 I know what most of you are probably thinking: the rule of 72? Have the Insurance Pro Blog guys run out of ideas for post topics? Or busy week? Maybe they didn’t have time to come up with something more creative than a boring post about a finance topic known the world over.
I know what most of you are probably thinking: the rule of 72? Have the Insurance Pro Blog guys run out of ideas for post topics? Or busy week? Maybe they didn’t have time to come up with something more creative than a boring post about a finance topic known the world over.
For those who don’t know the rule of 72 is a simple rule of thumb used to determine the amount of time an investment will take to double given a certain interest rate. You simple divide 72 by the given interest rate and boom you have the number of years it will take the investment to double.
Simple enough, and no real need to labor this issue any further. So, happy Monday and we’ll be back to you on Wednesday when the next episode of the Financial Pro Cast goes live.
Unless of course, the Rule of 72 is wrong…
What if Everything you thought was True Turned out to be Untrue?
Oh crap, here I thought I had at least one thing about life figured out. Sure life can be complicated. Is milk bad or good for you? Will eggs destroy your arteries with all their cholesterol? Are carbs good or bad? Are stocks a good bet for retirement savings? Does a 15-year mortgage really save me money?
With all these unanswered questions, I thought for a second that at least I could rely on one simple concept that has been known since at least the 1400’s. Nope turns out like all things, nuance plays an important role and as such, you should plan accordingly.
The Rule is Wrong
So the Rule of 72 is wrong? How wrong? And if so, why the hell does everyone still use it? The quick answers for those in a rush are: yes, depends on the interest rate, and convenience.
Let’s start backwards in answering these questions in a tad more detail.
72, the Lazy Man’s Calculator
The actual formula used to calculate precise doubling time of an investment is as follows:
That mathematical notation “ln” might scare some people off, but it simply denotes the natural log—aka log base e the mathematical constant. For those of you who are shaky with logarithms, they merely solve for the exponent of a given number. Most scientific calculators will give you quick access to two log functions: natural and base 10. Base 10 is a common logarithmic function due to our numbering system, but is of relatively little use to today’s discussion so we’ll skip those details.
The exact purpose behind the use of the natural log here dives into some deep mathematics that would likely make the majority of you leave, so for simplicity’s sake, let’s just say it’s been tested and proven that the nature log is what we want.
Simplifying our Formula a Bit More
There are times when access to a calculator may be limited, so a simplified version of our formula for calculating doubling times given a rate of interest would be handy. If we look back at the formula above, we might quickly determine that simply dividing an interest rate by the natural log of 2 should do the trick. There’s just one problem with that, the natural log of 2 is 0.69.
69 has four divisors: 1, 3, 23, and 69. That doesn’t make for very simply math in my head when it comes to quickly estimating doubling times for a rate of interest. So what do we have when we move up or down from 69?
On the way down we have 68 with 6 divisors, 67 a prime number (yuck), and 66 with 8 divisors. Moving up we have 70 with 8 divisors (not bad), 71 another prime number (yuck) and 72 with 11 divisors (jackpot). 72 is the closest number to 69 with the highest number of divisors, meaning we can more easily estimate doubling times in our head and get a nice even number.
How Wrong could it be?
The Rule of 72 is pretty good for interest rates between 6 and 10%. Outside of that range and it begins to degrade rather rapidly with respect to accuracy. There are a number of adjustments one can make to the numerator to make the estimation more accurate, but that doesn’t make for an easy calculation in one’s head, and I would argue is way more complicated than simply remembering: natural log of 2 divided by natural log of 1 plus the interest rate.
And if you’re reading this wondering to yourself “but what is the likelihood that I’ll happen to be carrying around a calculator with logarithmic functions on it when I need to calculate this?” here’s a really good tip. Take out your iPhone (something like 50% of all US teenagers have one, now), open up the calculator app, and turn your phone sideways. Voilà, you now have all the tools you need to calculate doubling times.
I don’t believe we really need to dive any deeper into that first question, the answer is simply yes, it’s wrong.
The Moral of the Story
I think I’ve mentioned a time or two that I really don’t like rules of thumb, and this is a perfect example explaining why. Very few people understand the serious limitations to the Rule of 72, let alone why those limitations exist. Just about every financial “expert” has quoted this rule from time to time, but I’m willing bet they don’t realize just how lucky they were that the example they used involved an interest rate between 6 and 10% (oh wait, Dave Ramsey like’s to talk about 12% average on mutual funds, and had use this rule to talk about doubling money in the past…woops Dave).
We’ve highlighted the point before, and we’ll continue to do so in the future, “expert” is a wildly over used term subject to broad interpretation. And this expert advice derived mostly from conventional wisdom without much room or time for critical minds can be dangerous. Because no matter how much you want it to be so, a 72% interest rate will not double your money in 1 year, it actually takes a little over a year and a quarter.


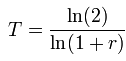
You see… you made me get out my Excel and make a spreadsheet again…
Hahahah!
And now you know precisely how long every interest rate from 1 to 99% will take to double an initial investment? 😉
I once took a math class in college that reflected a lot of the points you made in this post. The professor discussed why 72 was so significant and demonstrated with many different scenarios. He actually said that a more significant value was like 70.122223 etc.