Internal rate of return (IRR) is a commonly quoted measurement when talking about whole life and universal life insurance. This is because IRR is well equipped to tell us what sort of return we are achieving on these types of life insurance. That answer, while very simple, satisfies the curiosity of most.
But the exact reason for using IRR to accomplish this goal is quite complex and an interesting discussion in financial mathematics. It's been quite some time since I last dove through a heady discussion of mathematic technicality. If you come to The Insurance Pro Blog for the laughs (sarcasm), I'm afraid to say this blog post might leave you a tad disappointed. If, on the other hand, you're one of the three who enjoys a good numerical thriller (sarcasm…again) then you're in for a treat.
What is Internal Rate of Return?
At its core, internal rate of return is a complex calculation of cash flows evaluated to arrive at the effective return achieved by pursuing an investment option. In order to understand IRR, you need to be in the right headspace, so you have to first think of investing as costs. In other words, all investments have costs (i.e. what you pay to partake in them).
The majority of people look at investments in a linear fashion. What I mean is, they assume a fixed “investment” and calculate the return based on the payoff of that investment. This is an accurate way to compute returns insofar as we're only concerned about the return during a very short time period and/or we always incur the same investment cost. Anything that ventures outside of these two required parameters forces us to either:
- Attempt to flatten the variations in investment costs
- Aggregate the time periods as one long time period
In some cases both are necessary. In either case, both approaches will result in slightly (at best) or significantly (at worst and much more likely) flawed conclusions. This is the case, because our crude adjustments to the input data will generate outputs that magnify the effect of the adjustments.
So internal rate of return is a method for accurately calculating returns based on both the reality of a varied investment cost and a longer time period. The exact formula looks like this:
To calculate actual IRR we'd set net present value (NPV) to zero and solve for r. Doing this long-form (by hand) is nearly impossible because we usually use this formula by plugging a guess number in for r and computing NPV.
If the net present value comes out to a figure at or near zero, we determine our guess of the resulting IRR. Not too tricky when dealing with a short number of time periods, but quite the task as t increases. Thankfully, computer software will handle this task quickly and will work to arrive at a true NPV = 0 by using non-integers.
Difference Between Internal Rate of Return and Compound Annual Growth Rate
For those who gain intermediate expertise in financial mathematics, we often see wide use of compound annual growth rate (CAGR) when discussing investment returns. Some people might use the specific term compound annual growth rate and some may not. The specific CAGR calculation itself only applies to the growth of something over a specified time period without any control for ???
The compound annual growth rate tells us the effective year-over-year return of a single or fixed contribution investment made over time. So CAGR can answer questions like:
- If Sam makes a $100,000 investment in 2010 that is worth $150,000 in 2019, what is his return for the entire 10 year period?
- If Lydia invests $5,000 per year from 2010 through 2019 and has $75,000 in 2019 what is her return for the 10 year period?
Using the calculation for compound annual growth rate, we can tell you that Sam achieved a 4.14% return over 10 years and Lydia achieved a 7.26% return over 10 years.
The easiest way to perform these calculations is with a calculator equipped to perform Time Value of Money (TVM) calculations. If you were forced to buy a TI-83 Plus calculator for high school math class you own a calculator with the capacity to do this. If you don't happen to own one of these, there are several much less expensive financial calculator options available. Lastly, anyone with Microsoft Excel also has the ability to easily perform TVM calculations.
The above examples are simply TVM solve for “RATE” scenarios.
By the way, we cover a good introduction to Time Value of Money in Predictable Profits, so if you'd like a crash course that also includes examples on how specifically to plug numbers into the calculations, you can check it out there.
So this is great, but what happens when the circumstances become more complex. What happens if Sam invests $50,000 in year one and then another $50,000 in year five and ends up with $120,000 in 2019?
What happens if Lydia invests $5,000 for the first three years, nothing for the next two years, $3,000 for the following year, and then $8,000 for the remaining years and ends up instead with $61,000? Calculating the rate of return over the same time period just became far more complex.
This is where knowing how to use the IRR calculation becomes helpful. The internal rate of return tells us that in these new scenarios, Sam achieves a rate of return of 2.29% and Lydia 4.23%.
But IRR is more powerful than just telling us the effective rate of return when someone varies the investments. It can also tell us what the effective return is when someone both puts money in and takes money out.
Suppose Sam invests $100,000 and takes $25,000 from his investment in year six resulting in a cash balance in year 10 of $110,000. This is another scenario where a simple CAGR calculation lacks the complexity to calculate his effective rate of return. IRR, however, can easily handle this scenario, his return by year 10 is 3.39%.
Let's assume that Lydia invests $5,000 per year, but in year six she too withdraws $25,000 from the investment; by 2019, she has $30,000 remaining. What is her effective return, or internal rate of return? It's 6.14%.
When we Say “Effective Rate of Return…”
When I use the term “effective rate of return” here I mean the year-over-year interest equivalent result. So in the above examples, the interest rate you see is the rate Sam and Lydia would need to earn each year on their investments in order to arrive at the same result in year 10.
This is also what we normally refer to as the geometric average.
Difference between Internal Rate of Return (IRR) and Return on Investment (ROI)
It sounds like IRR focuses on the returns achieved on investments, so why can't we just use a return on investment calculation? Is there a difference? There sure is.
Return on investment is a simple calculation that measures the growth of a lump sum investment. You use ROI when you need to answer the following questions:
Jim invested $50,000 in Amazon in 2014 and sold his entire investment in 2018 for $65,000. What was Jim's total return on investment? The answer is 30%. The return on investment calculation is simply a percentage change calculation:
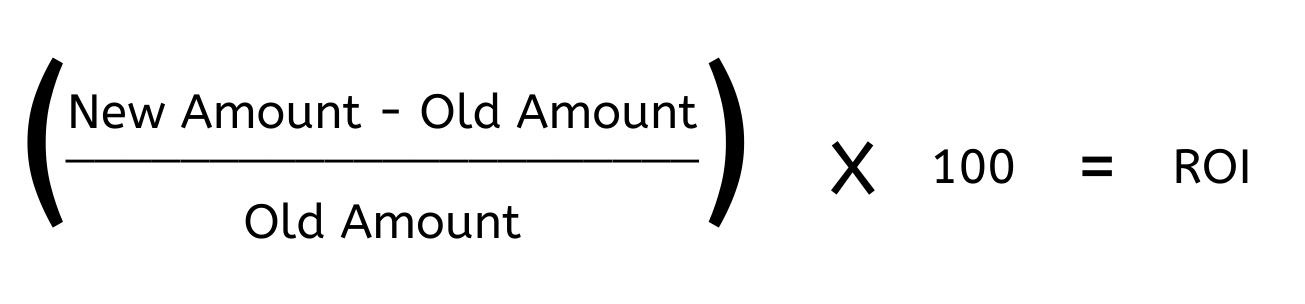The ROI calculation tells us the percentage of growth achieved by making the investment, but it does not account for the time that passed between initial investment and exit. If we wanted to know what the effective return on investment was for Jim, we don't need IRR. We can simply use the RATE solution for TVM. His year-over-year rate of return is 5.39%.
This calculation also lacks the ability to handle more complexity like partial liquidation. What if Jim sold half of his investment in 2018 for $25,000 and then the remaining investment in 2019, receiving $30,000 in total in 2019.
That question is too complex for the simple ROI calculation to answer. The IRR calculation, on the other hand, answers it easily. His effective year-over-year rate of return is 1.89%
Why Internal Rate of Return Matters for Life Insurance
When we evaluate life insurance, we have to evaluate against the other options we have to achieve the same goal. People often compare life insurance against investments of all sorts to determine if the values achieved by the life insurance contract are better, worse, or the same as the anticipated results achieved elsewhere.
The most commonly accepted metric that compares financial vehicles, is the year-over-year growth of its values. Life insurance can be a tad complex when it comes to inflows and outflows. While some people might pay a set premium for a number of years and simply want to know what the effective return is on the cash value and/or death benefit, many more people don't follow a straight line of paying the premium.
For example, if you own a 10 Pay whole life policy and wish to know what the effective rate of return achieved in year 25 is, you have to have a mechanism to account for 10 years of inflows, followed by 15 years of no inflows. Should you decide to take a loan against the policy in year 18, you also need a mechanism to account for this.
The internal rate of return is the only financial calculation that can do this with precision. Once you know the answer, you can compare it to the results you'd expect from other options and determine if life insurance is a good or bad option for you.
But take note that this means you have to be careful about the way in which you evaluate your alternative options. People often confuse the rate of return. As you can see from above, there are a few ways to calculate a “return” on an investment. There are also a number of ways one can approach the act of investing.
